| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- Apache
- 논문리뷰
- 머신러닝
- 수동설치
- Crawling
- image
- 딥러닝
- MySQL
- 한빛미디어
- 예제중심HTML&자바스크립트&CSS
- AndroidStudio를활용한안드로이드프로그래밍
- 한빛아카데미
- 소스설치
- deeplearning
- jupyter
- Selenium
- 셀레니움
- 밑바닥부터시작하는딥러닝
- word2vec
- 가비아
- 밑바닥부터시작하는딥러닝2
- 프로그램새내기를위한자바언어프로그래밍
- Lamp
- aws
- 비지도학습
- attention
- 크롤링
- CBOW
- 컴파일설치
- 생활코딩
- Today
- Total
안녕, 세상!
2. 퍼셉트론 본문
1. 퍼셉트론의 정의
'인공뉴런' 혹은 '단순 퍼셉트론'으로 불리며 다수의 신호를 입력으로 받아 하나의 신호를 출력합니다.

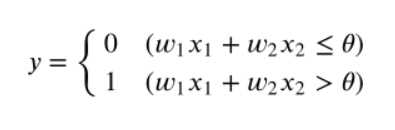
X1, X2는 입력신호, Y는 출력신호, W1,W2(Weight) 가중치, 세타는 임계값,
원은 뉴런 혹은 노드라고 부릅니다.
2. 단순 논리 회로 퍼셉트론 구현
(1) AND 게이트
| X1 | X2 | Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
입력인 X1,X2 두개 모두가 1일 경우에만 출력인 Y가 1입니다.
입력이 2개이고 출력이 1개인 퍼셉트론 형태로 AND 게이트를 코딩하면 다음과 같습니다.

편향 도입
기존의 식에서 임계값인 세타를 -b로 치환하면서 퍼셉트론의 동작이 다음과 같은 식으로 될 수 있습니다.

여기서 b부분을 편향이라고 합니다.
이제 편향을 도입하여 AND게이트를 다시 코드로 표현하면 아래와 같습니다.

np.sum() 함수 - 배열 원소간의 합을 내어주는 함수
형식: np.sum(배열변수) ex) a=[1,2,3,4]인 경우 np.sum(a)의 결과는 10
1. 배열이 1차원인 경우 - 위와 같이 배열의 원소들의 합을 출력함
2. 배열이 2차원인 경우 - 행의 원소들의 합과 열의 원소들의 합으로 나뉘어짐
①같은행의 원소들 합인 경우 axis=1
②같은열의 원소들 합인 경우 axis=0

(2) OR, NAND 게이트
마찬가지로 퍼셉트론 수식을 이용해 단층 퍼셉트론으로 OR게이트와 NAND게이트를 표현할 수 있습니다.
① OR
| X1 | X2 | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |

② NAND
| X1 | X2 | Y |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |

(3) 단층 퍼셉트론의 한계 (XOR 게이트 구현)
기존의 AND, OR, NAND 게이트는 입력층과 출력층이 각각 1층으로만 이루어진 단층 퍼셉트론만으로
구현이 가능했지만, XOR 함수는 단층 퍼셉트론으로 구현을 할 수 없습니다.
| X1 | X2 | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
하지만 기존 게이트(AND, OR, NAND)들을 조합하여 다층 퍼셉트론으로 XOR 게이트를 구현할 수 있습니다.

| X1 | X2 | K1 | K2 | Y |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 |
따라서 XOR을 코드로 표현하면 아래와 같습니다.

여기서 NAND, OR, AND 게이트 코드는 위의 코드를 이용했습니다.
XOR 게이트를 다층 퍼셉트론으로 구현을 했는데 퍼셉트론을 그리면 아래와 같습니다.

단층 퍼셉트론으로 표현하지 못하는 것을 다층 퍼셉트론으로 표현할 수 있으므로 비선형적 표현이 가능하며
이렇게 퍼셉트론을 이용해서 심지어 컴퓨터도 만들 수 있습니다.
'It공부 > Deep learning' 카테고리의 다른 글
| 5. 오차역전파법 (0) | 2020.06.19 |
|---|---|
| 4. 신경망 학습 (0) | 2020.06.17 |
| 3-(1) 손글씨 숫자 인식 분석 (1) | 2020.06.16 |
| 3. 신경망 (0) | 2020.06.16 |
| 1. Python 심화( Numpy, Matplotlib) (1) | 2020.06.13 |




