| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 딥러닝
- 셀레니움
- 소스설치
- 컴파일설치
- 수동설치
- 밑바닥부터시작하는딥러닝
- attention
- deeplearning
- Crawling
- 예제중심HTML&자바스크립트&CSS
- 머신러닝
- Lamp
- MySQL
- aws
- 가비아
- Apache
- jupyter
- Selenium
- CBOW
- 논문리뷰
- word2vec
- 밑바닥부터시작하는딥러닝2
- 프로그램새내기를위한자바언어프로그래밍
- 생활코딩
- image
- 크롤링
- 비지도학습
- 한빛미디어
- AndroidStudio를활용한안드로이드프로그래밍
- 한빛아카데미
- Today
- Total
안녕, 세상!
비지도 학습 - (1) K-means 기법 본문
(1) 클러스트링 (Clustering)
비지도 학습은 지도학습과는 다르게 입력 데이터들에 대한 정답 레이블이 없습니다.
따라서 입력 데이터들에 대한 특징들을 기반으로 연관성에 따라 정답 없이 분류를 해야 합니다.
즉, 클러스트링은 입력 데이터가 비슷한 것 끼리 클래스를 나누는 것입니다.
입력 데이터들이 넓은 범위로 흩어져 분포해 있을 것인데 데이터의 분포 모양을 클러스터(Cluster)라고 합니다.
데이터 분포에서 클러스터를 찾아, 동일한 클러스터에 속하는 데이터들은 같은 클래스로 분류하고 다른 클러스트에 속하는 데이터들은 다른 클래스를 할당하는 것이 클러스터링입니다.
(2) K-means
K-means 기법은 분류할 클러스터 수(K) 를 직접 정하고 클러스터 수 만큼의 중심 벡터(점)를 가지고 중심 벡터들을 입력 데이터들 사이에 제일 적합한 위치에 놓음으로써 입력 데이터들에 대한 클러스터를 분류하는 기법입니다.
K-means 기법에서는 세 변수를 사용합니다.
K : 클러스터 수
μ : 중심 벡터
R : 클래스 지시 변수 - 입력 데이터들이 어느 클러스터에 속해 있는지 알려주는 변수
ex) 지도 학습 정답레이블 one-hot-encoding 기법 [1,0,0]
① K-means 기법의 과정
Step (1)
클러스터의 수 K를 정하고 중심벡터 μ로 클러스터의 중심 위치를 적절하게 설정합니다.
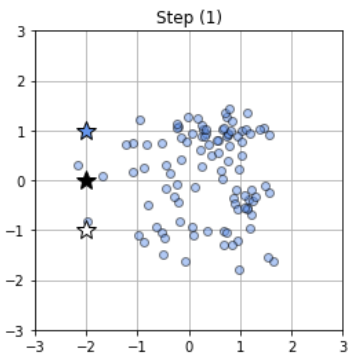
Step (2)
현 시점에서 클러스터의 중심 벡터 μ를 바탕으로 클래스 지시 변수 R을 결정합니다.
(입력 데이터들 마다 각 클러스터의 중심벡터 까지 거리를 측정 후 가장 가까운 중심벡터가 해당 입력 데이터의 클러스터로 결정함)
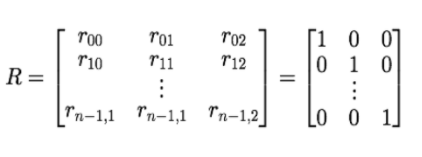
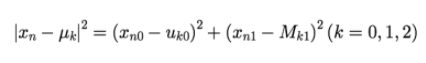

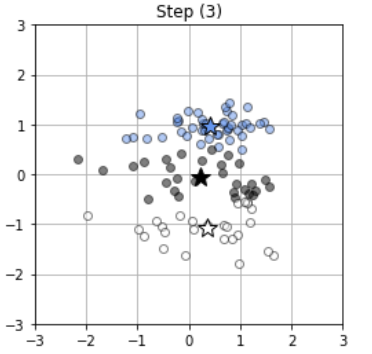
Step(3)
현 시점에서 클래스 지시 변수 R를 바탕으로 μ를 갱신합니다.
(Step(2)에서 입력데이터들의 결정된 클러스터들 끼리의 각 위치의 평균을 구하면 해당 클러스터의 중심 벡터를 구할 수 있음. 그러므로 그 중심벡터로 갱신함.)
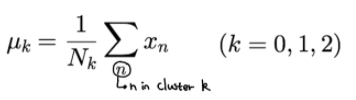
Step(4)
μ와 R이 수렴할 때 까지 Step(2)와 Step(3)를 순차적으로 계속 반복합니다.

중심 벡터와 클래스 지시 변수의 변화가 거의 없고 수렴할 때 반복을 멈추면 됩니다.
② 왜곡 척도
위의 K-means 과정을 보면 지도학습의 손실 함수(목적 함수)와 같이 학습이 진행됨에 따라 감소하는 함수가 없었습니다.
하지만, K-means도 손실함수를 가지고 있습니다.
K-means의 경우 입력 데이터들의 점이 속한 클러스터의 중심까지의 제곱 거리를 모두 합한 것으로 손실함수를 사용합니다.

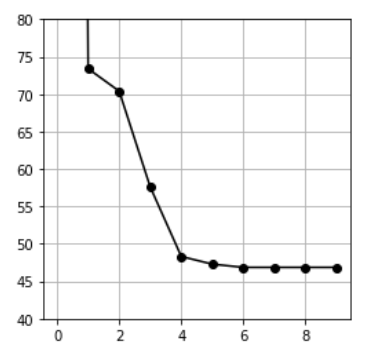
R을 갱신 한 후 왜곡 척도 J의 그래프입니다.
Step(2)와 Step(3)을 6번 정도 반복하면 J값이 어느정도 수렴함을 확인할 수 있습니다.
K-means 기법으로 얻을 수 있는 해는 초기값 의존성이 있습니다.
즉, μ와 R에 처음에 무슨 값을 할당하는지에 따라서 결과가 달라질 수 있습니다.
그러므로 다양한 μ 혹은R에서 시작하여 얻은 결과 중 왜곡 척도가 가장 작은 결과를 사용하는 방법이 사용됩니다.
(본 정리는 '파이썬으로 배우는 머신러닝의 교과서' 학습을 바탕으로 정리하였습니다.)
'It공부 > Machine Learning' 카테고리의 다른 글
| 비지도 학습 - (2) 확률적 클러스터링, 머신러닝에서의 가능도(Likelihood) (0) | 2021.01.04 |
|---|

